Από την αρχή ακόμα, την εποχή δηλαδή που τέθηκαν τα πρώτα θεμέλια των μαθηματικών, η επιστήμη αυτή χωρίστηκε σε δύο μεγάλους κλάδους· την Αριθμητική και την Γεωμετρία. Η μελέτη των σχημάτων και των ιδιοτήτων τους ήταν πάντα μια προσφιλής ενασχόληση των μαθηματικών όλων των εποχών. Σε αντίθεση όμως με τον κλάδο που ασχολείται με τους αριθμούς η Γεωμετρία έχει το μεγάλο πλεονέκτημα να είναι εξίσου δημοφιλής και στους μη έχοντες ιδιαίτερες μαθηματικές γνώσεις.
Στα μαθηματικά, το σχήμα θα παίζει πάντα πρωταγωνιστικό ρόλο. Από τα πιο απλά όπως το τρίγωνο, η σφαίρα και ο μαίανδρος μέχρι και τα πιο πολύπλοκα, τα γεωμετρικά σχήματα ασκούν μια παράξενη γοητεία στο ανθρώπινο πνεύμα. Δεν είναι λοιπόν παράξενο που από την αρχαιότητα η μελέτη της γεωμετρίας συνδέθηκε με όλες σχεδόν τις εκδηλώσεις του ανθρώπινου πολιτισμού. Οι πυραμίδες για παράδειγμα πολύ συχνά χρησιμοποιηθήκαν ως θρησκευτικοί χώροι και πολλά σχήματα όπως ο μαίανδρος που προαναφέρθηκε, χρησιμοποιήθηκαν για τον διάκοσμο των ναών. Οι Πυθαγόρειοι εκτός από τις πολλές μυστικιστικές αντιλήψεις που είχαν για τα σχήματα, συσχέτιζαν την μελέτη τους και με την Αστρονομία, την οποία αποκαλούσαν Γεωμετρία σε κίνηση. Ο Πλάτωνας στην είσοδο της φιλοσοφικής του σχολής είχε μια πολύ κολακευτική για την επιστήμη της Γεωμετρίας επιγραφή, «Μηδείς αγεωμέτρητος εισίτω» που σημαίνει σε ελεύθερη απόδοση «όποιος δεν γνωρίζει γεωμετρία να μη εισέλθει». Αυτή η επιγραφή φυσικά, δεν τέθηκε ως απαγόρευση αλλά για να καταδείξει την σπουδαιότητα της γεωμετρίας ως βασική προϋπόθεση για την τέχνη της φιλοσοφίας. Όσο για την τέχνη γενικότερα, αυτή είναι η κατεξοχήν ανθρώπινη δραστηριότητα που επηρεάζεται από την γεωμετρία. Τον 20ο αιώνα μάλιστα φτάσαμε στο σημείο να δημιουργηθεί μια τεχνοτροπία στη ζωγραφική που ονομάστηκε Κυβισμός. Τόσο επαναστατική ήταν αυτή η νέα τεχνοτροπία που η ίδια και οι εκπρόσωποί της έγιναν παγκοσμίως γνωστοί. Ακόμα και όσοι από εσάς αγνοείτε τι ακριβώς είναι ο κυβισμός σίγουρα γνωρίζετε τουλάχιστον ένα εκπρόσωπο του, τον Πάμπλο Πικάσσο.
 Άλλος όμως είναι ο ζωγράφος του οποίου ένα μεγάλο μέρος του έργου του είναι κυριολεκτικά μια γεωμετρική πανδαισία. Πρωτοπόρος της λεγόμενης αφηρημένης ή ανεικονικής ζωγραφικής ο Βασίλη Καντίνσκι έδωσε με τις καινοτομίες του και την νέα αντίληψη που κόμιζε για την ζωγραφική, μιαν άλλη πορεία στη τέχνη του 20ου αιώνα. Άνθρωπος με τεράστιες τεχνικές ικανότητες και βαθύτατο λυρισμό ο Καντίνσκι θεωρείται πια στις μέρες μας καλλιτεχνική μεγαλοφυΐα και ένας από τους σημαντικότερους καλλιτέχνες τις εποχής του. Ωστόσο δεν είναι μονάχα οι πίνακές του που τον καθιέρωσαν ως έναν από τους μεγάλους του περασμένου αιώνα. Στη πραγματεία του Για το Πνευματικό στην Τέχνη καταγράφονται οι θεωρίες και οι ιδέες που υποστηρίζουν την τάση του προς το αφηρημένο. Η εργασία του αυτή μαζί με κάποιες άλλες όπως τα βιβλία του Τέχνη και καλλιτέχνες και Σημείο-Γραμμή-Επίπεδο τον καθιστούν ένα από τους σημαντικούς θεωρητικούς της τέχνης, δίνοντας του ακόμα μεγαλύτερη αίγλη.
Άλλος όμως είναι ο ζωγράφος του οποίου ένα μεγάλο μέρος του έργου του είναι κυριολεκτικά μια γεωμετρική πανδαισία. Πρωτοπόρος της λεγόμενης αφηρημένης ή ανεικονικής ζωγραφικής ο Βασίλη Καντίνσκι έδωσε με τις καινοτομίες του και την νέα αντίληψη που κόμιζε για την ζωγραφική, μιαν άλλη πορεία στη τέχνη του 20ου αιώνα. Άνθρωπος με τεράστιες τεχνικές ικανότητες και βαθύτατο λυρισμό ο Καντίνσκι θεωρείται πια στις μέρες μας καλλιτεχνική μεγαλοφυΐα και ένας από τους σημαντικότερους καλλιτέχνες τις εποχής του. Ωστόσο δεν είναι μονάχα οι πίνακές του που τον καθιέρωσαν ως έναν από τους μεγάλους του περασμένου αιώνα. Στη πραγματεία του Για το Πνευματικό στην Τέχνη καταγράφονται οι θεωρίες και οι ιδέες που υποστηρίζουν την τάση του προς το αφηρημένο. Η εργασία του αυτή μαζί με κάποιες άλλες όπως τα βιβλία του Τέχνη και καλλιτέχνες και Σημείο-Γραμμή-Επίπεδο τον καθιστούν ένα από τους σημαντικούς θεωρητικούς της τέχνης, δίνοντας του ακόμα μεγαλύτερη αίγλη. Σαράντα περίπου χρόνια μετά το θάνατο του Καντίνσκι, ο Μπενουά Μάντελμπροτ ένας Γάλλος μαθηματικός, Πολωνικής καταγωγής, μας παρουσίασε κάποιους άλλους αναπάντεχους «μαθηματικούς καλλιτέχνες,» οι δημιουργίες των οποίων ξεπερνούν σε φαντασία, ευρηματικότητα αλλά και πολυπλοκότητα τα έργα πολλών απλών ζωγράφων. Στο βιβλίο Η μορφοκλασματική γεωμετρία της φύσης που εκδόθηκε το 1982 έχει συγκεντρώσει ένα πλήθος εκπληκτικών σχημάτων που δημιουργήθηκαν από ηλεκτρονικούς υπολογιστές ακολουθώντας μια πολύ απλή επαναληπτική διαδικασία. Τα σχήματα αυτά ονομάστηκαν από τον Μάντελμπροτ Fractals, στα ελληνικά Μορφοκλασματικές Δομές, και είναι κατά κάποιο τρόπο γραφικές παραστάσεις κάποιων εξισώσεων. Το βιβλίο αυτό σημείωσε τόσο μεγάλη επιτυχία που μέχρι σήμερα δεν υπάρχουν πολλά βιβλία μαθηματικών που να γνώρισαν τέτοια αποδοχή απ’ το ευρύ κοινό .
Σαράντα περίπου χρόνια μετά το θάνατο του Καντίνσκι, ο Μπενουά Μάντελμπροτ ένας Γάλλος μαθηματικός, Πολωνικής καταγωγής, μας παρουσίασε κάποιους άλλους αναπάντεχους «μαθηματικούς καλλιτέχνες,» οι δημιουργίες των οποίων ξεπερνούν σε φαντασία, ευρηματικότητα αλλά και πολυπλοκότητα τα έργα πολλών απλών ζωγράφων. Στο βιβλίο Η μορφοκλασματική γεωμετρία της φύσης που εκδόθηκε το 1982 έχει συγκεντρώσει ένα πλήθος εκπληκτικών σχημάτων που δημιουργήθηκαν από ηλεκτρονικούς υπολογιστές ακολουθώντας μια πολύ απλή επαναληπτική διαδικασία. Τα σχήματα αυτά ονομάστηκαν από τον Μάντελμπροτ Fractals, στα ελληνικά Μορφοκλασματικές Δομές, και είναι κατά κάποιο τρόπο γραφικές παραστάσεις κάποιων εξισώσεων. Το βιβλίο αυτό σημείωσε τόσο μεγάλη επιτυχία που μέχρι σήμερα δεν υπάρχουν πολλά βιβλία μαθηματικών που να γνώρισαν τέτοια αποδοχή απ’ το ευρύ κοινό . Τι είναι όμως μια Μορφοκλασματική Δομή; Καταρχάς είναι ένα σχήμα τόσο πολύπλοκο που δεν μπορεί να οριστεί με τους κανόνες και τους όρους της κλασικής ευκλείδειας γεωμετρίας. Ο ορισμός του γίνεται με βάση μιαν επαναληπτική διαδικασία και η δημιουργία του, συνήθως, με την ευεργετική συνδρομή των ηλεκτρονικών υπολογιστών. Ένα από τα βασικότερα χαρακτηριστικά του είναι η αυτό-ομοιότητα σε διάφορες κλίμακες. Με τον όρο αυτό-ομοιότητα εννοούμε ότι με μεγέθυνση σ’ ένα οποιοδήποτε σημείο του μπορούμε να δούμε είτε ολόκληρο το ίδιο το σχήμα είτε απλά ένα μέρος του.
Τέτοια σχήματα όπως προαναφέρθηκε είναι αποτέλεσμα μίας επαναληπτικής διαδικασίας, που συνήθως είναι πολύ απλή. Δείτε για παράδειγμα την κατασκευή του τάπητα του Σιερπίνσκι, μιας από τις πρώτες μορφόκλασματικές δομές που δημιουργήθηκαν. Ο τάπητας του Σιερπίνσκι δημιουργείται αφαιρώντας διαδοχικά το μεσαίο τετράγωνο από το μεγαλύτερο τετράγωνο που ήδη υπάρχει.
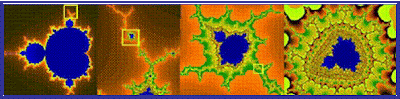
Αν όμως αντικαταστήσουμε αυτή την επαναληπτική διαδικασία με μιαν άλλη και προσθέσουμε χρώματα μπορεί να προκύψουν υπέροχα σχήματα. Το σύνολο του Μάντελμπροτ που φαίνεται παρακάτω είναι ένα από αυτά. Παρατηρήσετε την αυτό – ομοιότητα που εμφανίζεται τόσο στην περιφέρεια όσο και στις λεπτομέρειες μ’ ένα κυριολεκτικά εκπληκτικό τρόπο.
Η αλήθεια όμως είναι πως οι πραγματικοί καλλιτέχνες δεν είναι ούτε οι μαθηματικοί τύποι που δημιουργούν αυτές τις γραφικές παραστάσεις ούτε βέβαια οι ηλεκτρονικοί υπολογιστές με την βοήθεια των οποίων τις σχεδιάζουμε, αλλά οι άνθρωποί που αναδεικνύουν αυτά τα αριστουργήματα. Αυτοί που επιλέγουν εκτός από τους κατάλληλους τύπους και τα σωστά χρώματα, αυτοί που μας δίνουν την ευκαιρία να απολαύσουμε τέτοια ομορφιά εκεί που πραγματικά δεν το περιμένουμε!
Μερικοί Σύνδεσμοι




Γειά σου Παντελή! Συγχαρητήρια για το site σου. Πολλοί καλλιτέχνες δείχνουν με τα έργα τους την αγάπη τους για τα μαθηματικά. Κάπου είχα διαβάσει ότι ο κυβισμός επηρέασε και την αρχιτεκτονική. Όταν πρωτοκατασκεύασαν τα ορθογώνια κτίρια ήταν μεγάλη καινοτομία.
ΑπάντησηΔιαγραφήΕύη Χ.
QUAD
ΑπάντησηΔιαγραφήSAMUEL BECKETT
Ο Beckett περιγράφει το Quad σαν «μπαλέτο για τέσσερα άτομα» και στην εκδοχή που έχει δημοσιεύσει ο Faber, σαν « ένα έργο για τέσσερις παίκτες, φως και κρουστά». Ο Beckett σπούδασε μαθηματικά και παρόλο που δεν ασχολήθηκε με ανώτερα μαθηματικά, έφτασε να γνωρίζει πολύ καλά τα βασικά στοιχεία των σειρών, της θεωρίας συνόλων και της λογικής. Καθαρά εμπνευσμένος από μία δυαδική Gray Code αριθμητική ακολουθία, η οποία χρησιμοποιείται κυρίως σε αναλογικά και ψηφιακά σήματα μετατροπής στις μηχανές ηλεκτρομηχανικής, ο Beckett θεωρεί τους ηθοποιούς του Quad σαν υποσύνολα ενός ν- συνόλου που είναι κανονισμένο σε κυκλική λίστα, έτσι ώστε το κάθε μονοσύνολο να εμφανίζεται μία φορά, δύο γειτονικά σύνολα να διαφέρουν εξαιτίας της πρόσθεσης ή της αφαίρεσης ενός μόνου στοιχείου και το μόνο στοιχείο που μπορεί να αφαιρεθεί να είναι εκείνο που ήταν πιο πολύ παρόν στα προηγούμενα αλλεπάλληλα σύνολα της λίστας. Για τον Alessandro Carboni το Quad ήταν μια αφορμή για να μελετήσει και να αναλύσει το μηδέν και τη λειτουργία του σε μια χορογραφική διαδικασία.
Το Quad (διάρκειας 15 λεπτών)κινηματογραφήθηκε για τη Γερμανική τηλεόραση και παρουσιάστηκε στις 8 Οκτωβρίου του 1981. Το Quad I & II είναι η πιο φορμαλιστική, γεωμετρική και συμμετρική δουλειά του Beckett. Κάθε παίκτης περιγράφει το μισό τετράγωνο διαγράφοντας την ασυμμετρία πλευράς και διαγωνίου, αποφεύγοντας το κέντρο, κάνοντας μία απότομη στροφή προς τα αριστερά. Στην αρχή μπορεί να φαίνεται ότι αποφεύγει ο ένας τον άλλον, αλλά σταδιακά συνειδητοποιούμε ότι το κέντρο, σαν ένα άδειο χωρικά αντικείμενο, γίνεται το σημείο μηδέν της κίνησης.
Το Quad δεν είναι το μοναδικό απροκάλυπτο εγχείρημα του Beckett που θέτει στη σκηνή τη γεωμετρία. Η σκέψη του αυτή ξεκινάει από το 1963 που μεταξύ άλλων εκδίδει το “J.M. Mime”. Σε αυτό το έργο, δύο ζευγάρια, γιος και πατέρας και γιος και μητέρα ( ο Beckett έγραψε ότι μπορεί ο ένας να κουβαλάει τον άλλον) προσπαθούν να περιγράψουν τον μεγαλύτερο αριθμό μονοπατιών μεταξύ των τεταρτημορίων του τετραγώνου για να φτάσουν στο κέντρο Ο (to arrive hack at center, O). «Ξεκινώντας από το Ο και επιστέφοντας στο Ο διανύοντας τον μεγαλύτερο αριθμό μονοπατιών» ,είναι η περιγραφή του Beckett για τη δράση. Το μοτίβο σε αυτό το έργο είναι αρκετά περίπλοκο. Στο Quad ο Beckett μεγεθύνει τα τρίγωνα και προσθέτει ρυθμό. Το θέμα επαναλαμβάνεται, αφού το κέντρο αποφεύγεται και δεν αναζητείται, και η καταπίεση της κίνησης ενισχύεται από τα μοχθηρά στριψίματα.
Το έργο
Η κίνηση κάθε παίκτη χωρίζεται σε 8 μέρη. Η διαδρομή είναι αριστερόστροφη και ακολουθεί τη λογική πλευρά-διαγώνιος- πλευρά-διαγώνιος- πλευρά-διαγώνιος- πλευρά-διαγώνιος. Η διαδρομή αυτή είναι μοναδική. Σε κάθε διαδρομή ο παίκτης περνάει μία φορά από τις τέσσερις πλευρές και δύο φορές από τις διαγωνίους. Αρχικά ξεκινάει ένας μόνος του μετά συμπορεύεται με έναν δεύτερο παίκτη, όπου κατά την εκκίνησή τους βρίσκονται σε διαδοχικές πλευρές, έρχεται στο τέλος της διαδρομής τους και ένας τρίτος παίκτης έχοντας τώρα και οι τρεις παίκτες εκκίνηση σε διαδοχικές πλευρές και με παρόμοιο τρόπο εισέρχεται και ένας τέταρτος. Στη συνέχεια στο τέλος της διαδρομής φεύγει ο πρώτος που μπήκε, στο τέλος της δεύτερης διαδρομής ο δεύτερος και συνεχίζοντας με όμοιο τρόπο απομένει ο τελευταίος παίκτης όπου τώρα αυτός κάνει μόνος του τη προσωπική του διαδρομή ξεκινώντας με αυτό τον τρόπο μια δεύτερη ακολουθία κινήσεων όπου πάλι μπαίνει ένας – ένας κ.λ.π.
Όταν ολοκληρωθούν τέσσερις ακολουθίες, κάθε παίκτης θα έχει κάνει από ένα σόλο, θα έχει συμπορευτεί με έναν από τους άλλους παίκτες (μάλιστα δύο από αυτά τα ζευγάρια θα συμπορευτούν δύο φορές), και θα έχει συνυπάρξει: δύο φορές με άλλους δύο με όλους τους δυνατούς συνδυασμούς και τέσσερις φορές με τους υπόλοιπους τρεις, πάλι με όλους τους δυνατούς συνδυασμούς.
(Σχόλια των:Alessandro Carboni και S.E. Contarski. Επιμέλεια: Εύη Χερουβείμ)
Σ' ευχαριστώ Εύη για τα καλά σου λόγια αλλά κυρίως για την εξαιρετικά ενδιαφέρουσα αναφορά σου στα Μαθηματικά του Μπέκετ
ΑπάντησηΔιαγραφήΕυχαριστώ και πάλι !!!